Satz des Pythagoras mit Erklärung, Formeln und Beweis

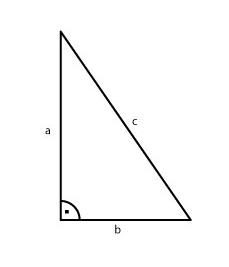
Der Satz des Pythagoras besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Katheten zum Quadrat gleich dem Flächeninhalt des Quadrats der Hypotenusen ist. Die Katheten sind hierbei die beiden kurzen Seiten des Dreiecks und die Hypothenuse ist die längste Seite des Dreiecks. Als Formel lautet der Satz des Pythagoras: a²+b²=c², wobei a und b die Katheten sind und c die Hypothenuse ist. Unten sehen Sie den Satz des Pythagoras anschaulich dargestellt und haben die Möglichkeit mit ihm zu rechnen.

Satz des Pythagoras berechnen
Einfach zwei Werte eingeben und der Dritte wird berechnet:
Umgeformte Formel
a
a²=√(c²-b²)
b
b²=√(c²-a²)
c
c²=a²+b²
Trigonometrische Funktionen

Aus dem Satz des Pythagoras lassen sich die sog. trigonometrischen Funktionen ableiten. Diese sind wie folgt definiert:

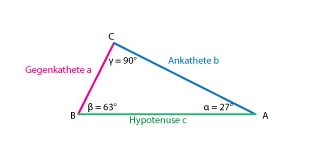
Wert Definition entspricht
sinα Gegenkathete von α
Hypothenuse		 a
c
cosα Ankathete von α
Hypothenuse		 b
c
tanα Gegenkathete von α
Ankathete von α 		a
b
sinβ Gegenkathete von β
Hypothenuse		 b
c
cosβ Ankathete von β
Hypothenuse		 a
c
tanβ Gegenkathete von β
Ankathete von β 		b
a

Fehler und Irrtümer vorbehalten. Alle Ergebnisse und Berechnungen ohne Gewähr.